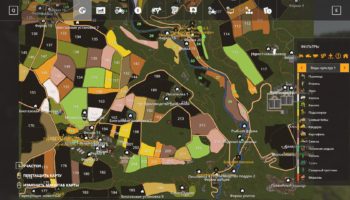
Farming Simulator 2019 настолько хорош, что трудно представить себе, что он может стать ещё лучше. И всё же это возможно - просто установите моды Farming Simulator 19. Да, именно так! Никто не может запретить вам усовершенствовать игру, потому что все моды абсолютно бесплатны. Каждый мод имеет своё предназначение, и их так много, что только когда вы попробуете их, вы поймёте, как много ограничений в этой игре. Множество улучшений, новые технологии и многое другое ждут вас.
Создайте свою собственную комбинацию модов FS 19 и посмотрите, как она будет работать. Возможно, именно вы создадите идеальную игру, в которой нет проблем. Так почему бы вам не попробовать? Устанавливайте моды FS 19 и сломайте все стереотипы о том, что эта игра не может быть лучше. Достигните совершенства и раскройте весь потенциал, который спит внутри вас!

В Ад на огонёк!
Далее

Vampire: The Masquerade — «Swansong» новая RPG от создателей «The Council»
Далее
League of Legends: главные события января
Далее

Охота на ренегата
Далее